HIMPUNAN & DIAGRAM VENN
himpunan dan diagram venn
Kata Pengantar
puji syukur penulis ucapkan atas kehadirat Allah SWT, karena dengan rahmat dan karunia-Nya saya masih diberi kesempatan untuk menyelesaikan tugas ini dengan baik walaupun masih terdapat kekurangan didalamnya. makalah Ini disusun agar pembaca dapat memperluas ilmu yang disajikan penulis berdasarkan pengamatan dari berbagai sumber. Dan setelah terselesaikanya makalah ini pembaca dapat memahami dan mengerti dalam penyusunan dan tata cara dalam mengerjakanya. Dan semoga bermamfaat…..
1. Pengertian Himpunan & macam-macam himpunan
a. Himpunan
Yang pertama kali mengenalkan himpunan adalah George Cantor (1845 – 1918), seorang ahli matematika dari Jerman. Ia menyatakan bahwa himpunan adalah kumpulan atas objek-objek. Objek tersebut dapat berupa benda abstrak maupun kongkret. Pada dasarnya benda-benda dalam suatu himpunan tidak harus mempunyai kesamaan sifat/karakter.
Kumpulan dari sebatang pensil, sebuah kursi dan setangkai bunga membentuk sebuah himpunan. Ketiga benda tersebut berupa benda kongkret, namun tidak memiliki kesamaan sifat. Benda-benda dalam suatu himpunan harus terdefinisi dengan jelas, well defined, artinya dapat dibedakan apakah suatu benda termasuk ataupun tidak dalam himpunan tersebut. Sebagai contoh, kumpulan semua bilangan genap membentuk sebuah himpunan, sebab syarat keanggotaannya terdefinisi dengan jelas.
Kumpulan orang-orang yang bodoh tidak merupakan himpunan sebab sifat “bodoh” tidak dapat didefinisikan dengan tepat. Akibatnya tidak dapat ditentukan secara pasti apakah seseorang guru matematika termasuk dalam himpunan tersebut atau tidak. Kenikmatan akan sebuah kopi juga bukan merupakan himpunan sebab penentuan kenikmatan tidaknya suatu bersifat subjektif, maksudnya tingkatan sebuah kenikmatan dari secangkir kopi dari setiap orang tidak bisa dianggap sama oleh pendapat orang lain.
Contoh termasuk dalam himpunan:
a. Kumpulan anak yang pintar dikelas ipa 1
b. Kumpulan anak yang rajin dikelas ipa 1
Contoh yang tidak termasuk himpunan ialah:
a. Kumpulan anak metal
b. Kumpulan anak remaja masjid
b. Penulisan macam-macam himpunan
Ada empat cara untuk menyatakan suatu himpunan yaitu sebagai berikut :
1. dengan menyebutkan semua anggotanya (roster) yang diletakkan di dalam sepasang tanda kurung kurawal, dan di antara setiap anggotanya dipisahkan dengan tanda koma. Cara ini disebut juga cara Tabulasi.
Contoh:
A = {2,13,4,5,6,7} |
B = { Rabu, Kamis, Jumat, Sabtu, Minggu,Senin,Selasa} |
2. menyebutkan syarat anggota-anggotanya, cara ini disebut juga cara Deskripsi.
Contoh :
{1,2,3,………,19} |
bilangan genap kurang dari 20 |
:
3. Notasi Pembentuk Himpunan : dengan menuliskan ciri-ciri umum atau sifat-sifat umum (role) dari anggotanya.
Contoh :
A adalah himpunan bilangan genap kurang dari sama dengan 40 |
Dengan notasi pembentuk himpunan, di tulis: |
{x|x ≤40, x bilangan genap } |
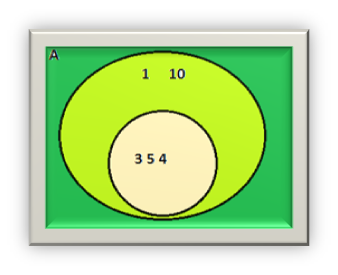
4. Himpunan juga dapat di sajikan secara grafis.
Contoh :
A = { 1,4,5,10}
B = {3,4,5}
2. Diagram venn dan operasi antara himpunan
a. Diagram venn
Diagram venn adalah suatu gambar yang digunakan untuk menyatakan suatu himpunan dalam himpunan semesta. Ciri dari diagram venn adalah adanya bilangan asli dan himpunan semesta. Contohnya:
Buat diagram venn jika
S = { 1, 2, 3, 4, 5, 6, 7, 8 }
A = { 1, 4, 6, 7 }
B = { 2, 4, 5, 8 }
b. Operasi antara himpunan
Gabungan(Union)
Gabungan dari A dengan B adalah A ∪ B = {x | x ∈
A atau x ∈ B}.
Irisan
Irisan dari A dan B adalah A ∩ B = {x | x ∈
A atau x ∈ B}.
Selisih
Selisih dari A dengan B adalah A-B = {x | x ∈
A ataux ∉ B}
Jumlah
Jumlah dari A dengan B adalah A+B = {x | x ∈ A ∪
B dan x ∉ A ∩ B}
3. Tabel macam-macam himpunan
4. Gambar hubungan diagram venn dan himpunan
Sudah mengerti cara membaca sekarang penulis akan memberi contoh gambar hubungan diagram venn dan himpunan, yaitu beriisan
Misalkan :
S: (1,2,3,4,5,6,7,8)
A: (1,2,5,6,8)
B: (2,4,5,7,8)
Diagram venn dari contoh di atas adalah
5. Bilangan bulat dan bilangan real
a. Bilangan bulat
Himpunan bilangan bulat didapatkan dengan menambahkan himpunan bilangan negatif ke dalam himpunan bilangan cacah. Sehingga, bilangan bulat terdiri dari ..,-3,-2,-1,0,1,2,3,…
Himpunan bilangan bulat juga dapat dibagi menjadi:
Bilangan bulat negatif, yaitu …, -10,-9,-8,-7,-6
Bilangan bulat positif, yaitu 1, 2, 3, …
Bilangan bulat non negatif, yaitu 0, 1, 2, 3,4,5,6,7,
Bilangan bulat non positif, yaitu …,-5,-4, -3, -2, -1, 0